“Solving problems is a practical art, like swimming, or skiing, or
playing the piano: you can learn it only byimitation and practice. . . . if you
wish to learn swimming you have to go in the water, and if you wish tobecome a
problem solver you have to solve problems.- Mathematical Discovery”
The undisputed father of mathematical problem solving is George
Pólya (December 13, 1887 – September 7, 1985), one of the giants of
classical analysis in the 20th century.
Pólya was born in Budapest, Hungary and died in Palo Alto,
California, almost 98 years later. Both of his parents were born Jewish but
converted to Catholicism. His father was born Jakab Pollák, a surname
suggesting Polish origins. Jakab changed his name to the more Hungarian ,
believing this would help him obtain his goal of a university position. He was
a talented solicitor, but because he often accepted cases without fees, he was
not a financial success. George, who was originally called György, attended
Dániel Berzsenyi Gymnasium, where he earned a fine academic reputation, but did
not shine in mathematics. Initially he resisted the career that fate had in
store for him, because as he later recalled his mathematics instructors who
should have been his models were “despicable teachers.”
Even at an early age George had great skill for analyzing and
solving problems. His uncle encouraged him to pursue a mathematical career but
Pólya wanted to become a lawyer like his father. He entered the University of
Budapest, became bored with all the legal technicalities he was required to
memorize. After reading Charles Darwin’s The Descent of Man, Pólya
briefly took up the study of biology,
but when his brother insisted there was no money to be made in the subject, George
shifted to languages and literature. Next he turned to philosophy but to better
understand it he had to learn mathematics and he was hooked. He was awarded a
PhD in mathematics from the University of Budapest (1912) for an essentially
unsupervised thesis in geometric probability. He spent the following year in
Göttingen.
Pólya’s first job was tutoring the son of a baron. His pupil
struggled with mathematics because he lacked problem-solving skills. To deal
with this Pólya began developing his method of problem solving, which he hoped
would not only work for his student but for others facing a similar challenge.
He was convinced that problem solving was not some special ability that some
are born with and others not, but rather was a practical skill that could be
taught to anyone, and if students are to have a chance of understanding
mathematics, it must be learned. In 1914 he was invited to teach at Zurich and
while in Switzerland he made two major discoveries. One was Stella Weber, with
whom he spent 67 years of married life. The second discovery came to him as he
took walks in a local park. It led to what he called the “random walk problem.”
Some years later he published a paper proving that if one continued a walk on a
grid long enough, one was certain to return to the starting point. In 1921 he
investigated what he called “street networks,” which are now referred to as
“lattices.”
In 1924 Pólya was the first International Rockefeller Fellow,
spending a year in England, where he worked with G.H. Hardy and John
Littlewood. Nine years later, he was once again a Rockefeller Fellow, spending
the year at Princeton University. Although his main mathematical interest was
in real and complex analysis, he also made contributions to probability,
combinatorics, algebra, number theory, voting systems and astronomy. Other
mathematicians’ elaborations on his major contributions have become the
foundations of several important branches of mathematics. Independently, Pólya
and Hilbert conjectured that the zeros of the Riemann zeta function correspond
to the eigenvalues of a self-adjoint Hermitian operator. His main contribution
to combinatorics is the enumeration theorem. He collaborated with Hardy and
Littlewood on the first systematic study of inequalities.
In 1940 George and Stella moved to the United States because of
their concerns about Hitler and the Nazis in Germany. He taught at Brown
University for two years, and then spent a short time at Smith College before
finally moving to Stanford in California, in 1942, where he stayed for the rest
of his life. He retired in 1954 but continued to teach until 1978. Pólya was a
masterful storyteller, a man of rare wit, insight, enthusiasm, and tremendous
curiosity. He was a genuinely friendly individual who enjoyed entertaining
visitors by showing them pictures of famous mathematicians he had known, and
recalling delightful and amusing instances in their lives. While Pólya was
correct in believing that he could teach others his skill for problem solving,
it is a shame that his other strengths can’t be taught as easily. In
“George (1887-1985),” Mathematics
Magazine, December 1987 M.M. Schiffer stated: “The driving force in his research was the search for beauty and the joy
of discovery.”
Books of
Polya:
which has been translated into 21 languages, has sold more than a
million copies over the years. with Pólya’s How To Solve It, they have
already developed their own strategies for learning mathematics. There seems to
be an extra principle that should be added to Pólya’s – one preceding number
four. That is, pretending you are interested in finding the solution of
a problem until you get to the point that you are. Teaching mathematics is
difficult for reasons that appear to be unique to the subject. One of these is
that there are several languages integral to the learning process with which
teachers and pupils alike must be conversant.
His Ten Commandments for Teachers, found in his book
Mathematical Discovery (1981) are as follows:
1. Be interested in your subject.
2. Know your subject.
3. Know about the ways of learning: the best way to learn anything
is to discover it by yourself.
4. Try to read the faces of your students, try to see their
expectations and difficulties, put yourself in their place.
5. Give them not only
information, but “know-how,” attitudes of mind, the habit of methodical work.
6. Let them learn guessing.
7. Let them learn proving.
8. Look out for such
features of the problem at hand as may be useful in solving the problems to
come – try to disclose the general pattern that lies behind the present
concrete situation.
9. Do not give away your
whole secret at once – let the students guess before you tell it – let them
find out for themselves as much as feasible.
10. Suggest it; do not
force it down their throats.”
A. What Is
Problem Solving?
Problem
solving and reasoning are now more prominent in school mathematics than ever
before. As we have stated previously, we believe that reasoning skills will be
developed through a continuous emphasis on problem solving. Students are
confronted by problems both in school and in their daily activities. For
example, in the classroom, problems are represented by the techer or from the
textbook.
A
problem is a situation, quantitive or otherwise, that confronts an individual
or group of individual, that requires resolution, and for which the individual
sees no apparent or obvious means or path to obtaining a solition. Using this
idea of the problem, problem solving emerges as a process. In fact,
It
(problem solving) is the means by which an individual uses previously acquired
knowledge, skills, and understanding to satisfy the demands of an unfamilar
situation.
Problem Solving also means engaging in a task for which the
solution method is not known in advance.
In order to find a solution, students must draw on their knowledge, and
through this process, they will often develop new mathematical
understandings. Solving problems is not
only a goal of learning mathematics but also a major means of doing so. Students should have frequent opportunities
to formulate, grapple with, and solve complex problems that require a
significant amount of effort and then be encouraged to reflect on their
thinking.
By learning problem solving in mathematics, students should
acquire ways of thinking, habits of persistence and curiosity, and confidence
in unfamiliar situations that will serve them well outside the mathematics
classroom. In everyday life and in the
workplace, being a good problem solver can lead to great advantages. Problem solving is an integral part of all
mathematics learning, and so it should not be an isolated part of the
mathematics program. Problem solving in
mathematics should involve all five content areas: Number and Operations, Algebra, Geometry,
Measurement, and Data Analysis & Probability.
Trying to find the solution, we may repeatedly change our point of
view, or way of looking at the problem. We have to shift our psition again and
again. Our conception of the problem is likely to be rather incomplete when we
start the wprk, our out look is different when we have made some progress, it
is again different when we have almost abtained the solution.
B. The Differences
of Problem and Task
Not everyone agrees on what exactly is a problem. There may not be
a perfect definition of “problem,” but it is possible to make a distinction
between a problem and a task. With a task, one knows what to do and how to do
it; with a problem, neither what to do nor how to do it may be known, at least
initially. One of the first steps in problem solving is to carefully describe
the problem one wishes to solve, and this may not be easy. Whereas in
classrooms, problems are presented to students to solve, in the real world,
problems are not ordinarily assigned by someone to be solved, but are
discovered to need solving. Even some of those successful in “solving”
problems, may not understand problems. Many have been taught to mimic a
procedure, and as good imitators they get correct answers, but may have little
awareness of what they have done or of the value of their labor.
If students merely imitate procedures, no plan is needed, and this
becomes obvious when they are asked to work on a new, unfamiliar problem. They
do not think about the problem or a plan of attack. Instead they ripple through
their Rolodex of memorized techniques, hoping to find a trick that works. For
them, carrying out a plan consists of mindlessly imitating the technique they
have learned. After they get an answer, they don’t look back, not even to see
if their result makes any sense in the context of the problem. As the primary
goal of good students is to understand things, it should be the goal of good
teachers to help others understand. This cannot be accomplished through
memorization or imitation. By the time some people become acquainted
There is the mathematics itself, the language of mathematics, the
language of logic, and a meta-language, which teachers use to instruct
students in the language of mathematics so that mathematics itself may be
understood. For instance, meta-language is used to provide students with an
intuitive understanding of mathematical concepts before they are formalized or
abstracted. By examining meta-languages used by teachers it is possible to
determine likely communication failures that prevent willing instructors from
helping willing students realize their mathematical potential in problem
solving
“A
mathematics teacher is a midwife to ideas.” – George Pólya
C. PROBLEM SOLVING STRATEGIES BY POLYA
In order to group conveniently the question and suggestions of our
list, we shall distinguish four phases of the work. Polya identifies four principles that form the basis
for any serious attempt at problemsolving:
SEE,
PLAN, DO, CHECK
1.
Understand the problem (SEE)
2.
Devise a plan (PLAN)
3.
Carry out the plan (DO)
4.
Look back (CHECK)
Each
of these phase has its importance. It may happen that a student hits
upon an axcptionally bright idea and jumping all preparation bluits out with
the solution. Such lucky idea, of course, are most desirable, but something
very undesirable and unfortunate may result if the student leaves out any of
the four phase whithout having a good idea. The worst may happen if the
students embarks upon computations or constructions whitout having seen the
main connection , or having made a sort of plan. Many mistakes can be avoided
if, carrying out his plan, the students checks each step. Some of the best
effects may be lost if the students fail to reexamine and to reconsider the
completed solution. For each phase will explain below :
1. Understand the problem
"Understand the problem" is often neglected as being obvious and
is not even mentioned in many mathematics classes. Yet students are often
stymied in their efforts to solve it, simply because they don't understand it
fully, or even in part. The students should
understand the problem. But he should not only understand it, he should also
desire its solution. If the student is lacking in understanding or interest, it
is not always his fault; the problem should be well chosen, not too difficult
and not too easy, natural and interesting, and some time should be allowed for
natural and interesting presentation. In order to remedy this oversight, Pólya taught teachers how to prompt each
student with appropriate questions, depending on the situation, such as:
·
What are
you asked to find out or show?
·
Can you
draw a picture or diagram to help you understand the problem?
·
Can you
restate the problem in your own words?
·
Can you
work out some numerical examples that would help make the problem more clear?
There are the way can you use to Understand the problem :
·
Carrefully
read the problem
·
Decide what
you are trying to do
·
Identify
the important data
The teacher is to select the question with the appropriate level of
difficulty for each student to ascertain if each student understands at their
own level, moving up or down the list to prompt each student, until each one
can respond with something constructive.
Then we chould subdivided
Understanding the Problem into two stages : “Getting
acquainted” and “Working for better understanding.”
Example
:
Let us illustrate
some of the points examplained in the foregoing section. We take the following
simple problem :
“Find the diagonal of rectangular
paraleleliped of which the length, the width, and the height are known.”
In order to discuss this problem
profitably, the students must be familiar with theorema pythagoras, and with
some of its applications in plane geometry, but they may have very little
systematics knowledge in solid geometry. The dialogue between the teacher and
the students may start as follows :
“What is the unknown?”
“the length of the diagonal of a
parallelepiped.”
“What are the data?”
“The length, the width, and the height of
the parallelepiped.”
“Introduce suitable notation. Which letter
shpuld denote the unknown?”
“x”
“which letters would you choose for the
length, the width, and the height?”
“a,b,c.”
“What is the condition, linking a,b,c and
x?”
“x is the diagonal of the parallelepiped of
which a,b,c are the length, the width, and the height
“Is it a reasonable problem? I mean, is the
condition sufficient to determine the unknown?”
“Yes, it is. If we know a,b,c we know the
paralleliped. If the parallelepiped is determined, the diagonal is determined.”
2. Devise a plan
In order to be able to see the student’s position, the teacher
should think of his own experience, of his difficulties and successes in
solving problem. We know, of course, that it is hard to have a good idea if we
have little knoledge of the subject, and impossible to have it if we have no
knowledge. Good ideas are based on past experience and formerly acquired
knowledge. Mere remembering is not enough for a good idea, but we cannot have
any good idea without recollecting some pertinent facts; materials alone are
not enough for constructing a house but we cannot construct a house
without collecting the necessery
materials. The materials necessary for solving a mathematical problem are
certain relevant items of our formerly acquired mathematical knowledge, as
formerly solved problems, or formerly proved theorems. Thus, it is often
appropriate to start the work with the question: Do you know a related problem?
Pólyamentions that there are many reasonable ways to
solve problems. The skill at choosing an appropriate strategy is best learned
by solving many problems. You will find choosing a strategy increasingly easy.
A partial list of strategies is included:
§ Gather together all available information
§ Consider some possible actions
§ Look for a pattern
§ Draw a sketch
§ Make an organised list
§ Simplify the problem
§ Guess and check
§ Make a tabke
§ Write a number sentence
§ Act out the problem
§ Identify a sub-task
§ Check the validity of given information
Example (continuous the example in number 1)
The dialogue between the teacher
and the students may start as follows :
“do you
know a related problem?”
.......
“look at the unknown! Do you know a problem
having the same unknown?”
“well, what is the unknown?”
“the diagonal of a parallelepiped.”
“do you know any problem with the same
unknown?”
.......
“you see, the diagonal is a segment, the
segment of a straight line. Did you never solve a problem whose unknown was the
length of a line?”
“of course, we have solved such problem. For
instance, to find a side of a right triangle.”
“good! Here is a problem related to yours
and solved before. Could you use it?”
..............
“you
were lucky enough to remember a problem which is related to your presents one
and which you solved before. Would you like to use it? Could you introduce some
auxiliary element in order to make its use possible?”
.............
“look here, the problem you remembered is
about a triangle. Have you any triangle in your figure?”
...........
“you cannot find yet the diagonal; but you
said that you could find the side of a triangle. Now, what will you do?”
“could you find the diagonal, if it were
side of a triangle?”
“I think that was a good idea to draw that
triangle.”
“the unknown is the hyphotenuse of the
triangle; we can calculate it by the theorem of pythagoras.”
“you can, if both legs are known; bu are
they?”
“one leg is given, it is c. And the other, I
think, is not difficult to find. Yes, the other leg is the hypothenuse of
another right triangle.”
“very good! Now I see that you have a plan.”
3. Carry out the plan
This step is usually easier than devising the plan In
general, all you need is care and patience, given that you have the necessary
skills. Persist with the plan that you have chosen. If it continues not to work
discard it and choose another. Don't be misled; this is how mathematics is
done, even by professionals
Carrying out the plan is
usually easier than devising the plan
Be patient – most problems are not solved
quickly nor on the first attempt
If a plan does not work
immediately, be persistent
Do not let yourself get
discouraged
If one strategy isn’t working,
try a different one
Example ( continuous the previous example)
The teacher has no reason
to interrupt the students if he carries out these details correctly except,
possibly, to warn him that he sould check each step. Thus, the teacher may ask
:
“can
you see clearly that the triangle with sides x,y,c is a right triangle?”
“but
can you prove that this triangle is a righ triangle?”
4. Look back (reflect)
Pólya mentions that much can be gained by taking the time
to reflect and look back at what you have done, what worked and what didn't.
Doing this will enable you to predict what strategy to use to solve future
problems, if these relate to the original problem
Does your answer make
sense? Did you answer all of the
questions?
What did you learn by
doing this?
Could you have done this problem another way
– maybe even an easier way?
Example( continuous the previous example)
The students finally
obtained the solution of the diagona is
The teacher can ask several question about the result which the
students may readily answer with “yes” or “no”
“did
you use all the data? Do all the data a,b,c appear in your formula for the
diagonal?”
“length,
width, and height play the same role in our question; our problem is symmetric
with respect to a,b,c. Does it remain unchanged when a,b,c are intercanged?”
“our
problem is a problem of solid geometry; to find the diagonal of a parallelepiped
with given dimensions a,b,c. Is the result of our ‘solid’ problem analogous to
the result of ‘plane’ problem?”
“if
you put c=0 in your formula, parallelepiped becomes a parallelogram. Do you
obtained the correct formula for the diagonal of the rectangular
parallelogram?”
A. APPLYING OF
POLYA’S PROBLEM SOLVING IN MATHEMATICS
1.
GUESS AND CHECK
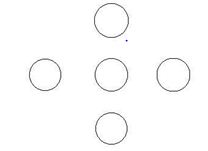
Copy the figure below and place the digits 1, 2, 3, 4, and 5 in these circles so that the sums across
(horizontally) and down (vertically) are the same. Is there more than one solution?
SOLUTION
:
Emphasize
Polya’s four principles- especially on the first several examples, so that
procedure becomes part of what the students knows.
1.
Understand
the problem.
Have the students
discuss it among themselves in their groups of 3, 4 or 5.
2.
Devise a plan.
Since we are
emphasizing Guess and Check, that will be our plan.
3.
Carry out
the plan.
It is best if you let
the students generate the solutions. The
teacher should just walk around the room and be the cheerleader, the
encourager, thefacilitator. If one solution
is found, ask that the students try to find other(s).
Possible solutions:
2 3 2
1 3 5 2 1 5 1 5 4
4 4 3
Things to discuss (it is best if the students tell you these
things)
·
Actually to
check possible solutions, you don’t have to add the number in the middle – you
just need to check the sum of the two “outside” numbers.
·
2 cannot be
in the middle, neither can 4. Ask the
students do discuss why.
4.
Look back.
Is there a better
way? Are there other solutions? Point
out that “Guess and Check” is also referred to as “Trial and Error”. However, I prefer to call this “Trial and
Success”, I mean, don’t you want to keep trying until you get it right?
Below is an exercise to
assign for the next day, which is also included in the STUDENTPROBLEMS.
1.
Put the numbers 2, 3, 4, 5, and 6 in the circles to make the sum across and the
sum down equal to 12. Are other
solutions possible? List at least two,
if possible
SOLUTION: One possibility 2
Other solutions
possible. 3 4 5
Have students suggest
those. 6
1.
MAKE AN
ORGANIZED LIST
Three darts hit this dart board and each scores a 1, 5, or 10.The
total score is the sum of the scores for the three darts.There could be three
1’s, two 1’s and 5, one 5 and two 10’s,And so on. How many different possible total scores
could aperson get with three darts?
SOLUTION:
1st. Understand the
problem.
Gee, I hope so. ☺ But let students talk about it just to make
sure.
2nd. Devise a
plan. Again, it would be what we are studying: Make an organized or
orderly list. Emphasize
that it should be organized. If students
just start throwing out
any combinations, they are either going to list the same one twice
or miss some
possibilities altogether.
3rd. Carry out the
plan.
There are 10 different possible scores.
4th. Look back.
Point out the there are other ways to “order”
the possibilities
List the 4-digit numbers that can be written using each of 1, 3, 5, and 7 once and only once. Which strategy did you use?
SOLUTION:
1357 1735 3517
5137 5713 7315
1375 1753 3571
5173 5731 7351
1537 3157 3715
5317 7135 7513
1573 3175 3751
5371 7153 7531
24 possible 4-digit numbers.
1.
MAKE A TABLE
Pedar Soint has a special package for large groups to attend their
amusement park: a flat fee of $20 and $6
per person. If a club has $100 to spend
on admission, what is the most number of people who can attend?
SOLUTION:
1st. Understand the problem.
Students may need to discuss this a little before attempting to
tackle the problem.
2nd. Devise a plan.
Make a table. But develop
what should be in the table with the students.
Let them
assist how you make this table.
3rd. Carry out the
plan.
Answer: At most, 13 people
can attend for $100 and they will have $2 l eft
over.
4th. Look back.
Is
there another way this could be done?
Yes, guess and check (whichis part of what we did). The difference is that we tried to do this in
an orderly fashion not just guess
randomly. We tried to “surround” the
solution.
Assign
the following problem.
Stacey had 32 coins in a jar.
Some of the coins were nickels, the others were dimes. The total value of the coins was $2.80. Find out how many of each coin there were inthe
jar. What problem solving strategy did
you use?
SOLUTION: 8 nickels, 24 dimes
References :
Polya,
George. 1957. How To Solve It : A New
Aspect of Mathematical Method. United state of America : Princeton
University Press, Princeton, New Jersey.
Polya, George.
1887. Mathematical Discovery. Canada : John Wiley & Sons.
Billstein, Rick. And friends. 2010. A problem Solving Approach to mathematics
for elementary School Teachers. United state of America : Pearson












0 komentar:
Posting Komentar